Batch 2 - Class 98 - Celtic Knots
Pre-Class Problem:
- (Dudeney - 76) A man bought an odd lot of wine in barrels and one barrel containing beer. These are shown in the illustration, marked with the number of gallons that each barrel contained. He sold a quantity of the wine to one man and twice the quantity to another, but kept the beer to himself. Which barrel contained the beer?
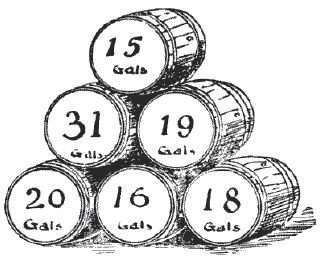
- Answer: 20 gallons. This can be solve by trial and error. Or by noticing that the quantity of wine sold is a multiple of three, where as the digital root of sum of all barrels is 2. Hence the beer barrel must have a digital root of 2 + 0,3,6 i.e. 2, 5, or 8. That is only true of 20 gallon barrel.
Attendance: Khushi, Anshi, Anisha, Anishka, Arnav, Muskaan, Tishyaa
Class Notes:
- Celtic Counting requires students to trace an under and over pattern – counting the Celtic loops. How many loops exist in this knot?
.png)
- Answer: Two
- How many loops does this knot have?
.png)
- Answer: Three
- Instructor Notes: Let kids try out a few other knots themselves
- Square Knot Patterns
- How many loops does the following knot pattern have?
.png)
- Answer: Six - each a rectangle
- Lets take a 6x7 knot - how many loops does this have?
.png)
- Answer: One!
- Lets take a 6x8 knot - how many loops does this have?
.png)
- Answer: Two
- How about a 6x9 knot?
.png)
- Answer: Three
- Any idea on what is going on? Can you try and guess the formula for square knots?
- Do you notice the symmetry? Following is the "center loop" and the two fishes.
.png)
- What can you say about symmetry in a nxm knot?
- Instructor Notes: Some kids may come up with notion of Greatest Common Divisor. Else motivate and take other examples like 6x12 or 5x10. Advanced kids may get the intuition and understanding
- Why does the GCD determine number of loops?
- For pxq knot, LCM(p,q) is where the knot will retrace itself. This represents pj=qk=LCM for some j and k. Number of loops is p/k (or q/j) which is GCD since GCD.LCM=pq
- Can also think of this as a pattern of the full knot repeated in a grid. So instead of bouncing off an edge, continue over on block. One will repeat on a loop after LCM/p heights or LCM/q widths, and by then the loop/straight line would have covered p/GCD points on left edge and q/GCD points on top edge of original grid. Since all p left-points have to be covered eventually, the number of loops is GCD.
- Solve some of the more advanced ones on the exercise sheet
- Draw your own loops! and solve!
Card Magic!
Trick: Deal three piles of three cards face-down. Have the victim choose a pile and turn it over to view the bottom card on the pile. Place the selected pile on top of the other two and spell out the name of the card as follows. Suppose the card is the 4 of spades. Spell out the words: “FOUR” “OF” “SPADES”. With each letter, deal a card from the top of your original pile face down onto a new pile. When the letters run out on a word, drop the rest of the remaining cards, in order, on top of the cards you spelled out. Do this three times, for each of the three words in the card’s name. Finally, spell out the word “MAGIC”, where the first four cards, corresponding to the letters “MAGI” are face down, but deal the final one, corresponding to the “C” IN “MAGIC”, face up. That will be the selected card.
Discussion: This works since the names of the cards have between 3 and 5 letters, no matter what the rank of the card: “ACE”, “TWO”, ..., “JACK”, “QUEEN”, “KING”. That means that since the selected card was the third one down, no matter what its name, it will be third from the bottom after the spelling of the rank. Spelling out “OF” always moves it two up in the deck, so it will be the middle card (fifth from the bottom). The suit names all have between 5 and 8 letters: “CLUBS”, “DIAMONDS”, “HEARTS” or “SPADES”, thus on the final spelling, the the fifth card (which is the selected card) will again be in position 5, no matter what. And the fifth card is the one selected by the spelling of “MAGIC”. A good way to demonstrate this is to make the selected card a different color so the students can see how it moves through the deals.
Homework
- Can you move as few cards as possible so that the total in the two columns becomes equal

- Answer: Swap 9 and 8, and turn 9 upside down!
References:
https://ia902701.us.archive.org/4/items/AmusementsInMathematicspdf/AmusementsInMathematics.pdf - Dudeney